Dijkstra’s Algorithm For Path Finding Problems

The blog is migrated to https://thiloshon.wordpress.com 
   
The path finding is one of the most common problems found in computer science, especially in game development and AI. The problem has been analyzed, scrutinized and dissected by various people and several possible solutions and algorithms have been implemented. The important part is not to implement one by ourselves but to understand what each does and how its effective from one another. In the CW, this is exactly what’s expected. You don’t necessarily have to implement the best solution. You just have to implement one and understand how efficient it is. I.e. derive the growth rate.  It can be a slow algorithm. If its slow say its slow and justify why its slow. Derive the growth rate and support your rationale.

I’m using the Dijkstra’s Algorithm in this blog to find the shortest distance path. Don’t be intimidated by the name of the Algorithm, its fairly simple one. It uses Greedy Algorithm with a simple tweak and is okayishly fast. Might not work effectively in large datasets with lots of blocks but that’s fine for now.

I’m using the StdDraw library provided in the ‘Algorithms, Part II’ Coursera Course by Princeton University and few additional code from the course. 

Alright, enough with the prepping, lets dive in. First let’s see if the algorithm makes sense.

Dijkstra’s Algorithm starts from the start node and checks for the best node surrounded by it. In our case the shortest distance node. It moves to that node and from that node checks the best node surrounded. Moves to that node. It does this repeatedly. Until it finds the destination. That’s it. Theory done, Class dismissed.

Dry Run

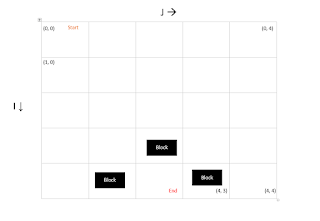
This is a sample grid with three blocks, Let’s find shortest distance from start on (0,0) to end on (4,2). 



The demo is done with Euclidean Distances in mind. So horizontal path gets the value 1 and diagonal paths get 1.4.
First we define the distance of start as 0 and all other grids as infinity.



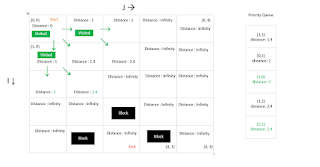
From the start grid, we set the minimum distance of the surrounding grids. The horizontal grid distance is 1. One is less than infinity. So we set 1 as distance of horizontal values. The diagonal value is 1.4. 1.4 is less than infinity. So we set diagonal grids’ distance as 1.4. Meanwhile we add the visiting nodes to a priority queue prioritized by the lesser distance value. And also we define the parent nodes of each node from which the minimum value was taken.





Once we find all node distances around the start node we set start node as ‘visited’. We won’t check visited nodes again.



Then we take the top node from the priority queue and change values surrounding that node. Here we add the distance of the current node to the value when finding distance to surrounding nodes.



At the end of 2nd node the values and parents are like this.



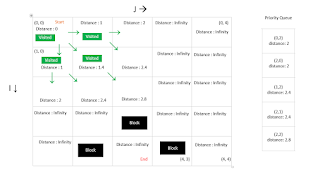
Then take the node from priority queue and do the same.



And again.



At the end of that iteration the values and parents are as follows.



Then we take the node from priority queue and do yet again.



And again.



You keep doing this until you hit the end node.



Once you get to the end node, trace back the parent nodes from the end to find the path. The distance is already found.



So that is how you find the shortest path in a grid.

The Code

/*************************************************************************
 *  Author: Thiloshon Nagarajah
 *  Created: 12-Dec-16
 *  Last update: 29-03-2017
 *
 * Path Finding using Dijkstra in Euclidean Distance
 *************************************************************************/

import java.util.*;

public class Dijkstra {

    Node start;
    Node end;
    Node[][] gridArea;

    // Horizontal and VerticalDistance
    double hVDistance = 1.0; 
    
    // Diagonal Distance
    double dDistance = 1.4; 

   /* for Manhattan Distances,
    double horizontalVerticalDistance = 1.0;
    double diagonalDistance = 2.0;

    for Chebyshev Distances,
    double horizontalVerticalDistance = 1.0;
    double diagonalDistance = 1.0; */

    /**
     *
     * @param matrix The boolean matrix from the framework given
     * @param si start x value
     * @param sj start y value
     * @param ei end x value
     * @param ej end x value
     * @return The path nodes
     */
    ArrayList<Node> distance(boolean[][] matrix, int si, int sj, int ei, int ej) {

        int size = matrix.length;

        start = new Node(si, sj);
        end = new Node(ei, ej);
        // The grid that is used to store nodes
        gridArea = new Node[size][size];

        // Creating nodes and finding blocked cells in matrix and mapping accordingly to our grid
        for (int i = 0; i < size; ++i) {
            for (int j = 0; j < size; ++j) {
                gridArea[i][j] = new Node(i, j);
                if (matrix[i][j] == false) {
                    gridArea[i][j].blocked = true;
                }
            }
        }

        // setting start distance to 0. 
        // All other nodes will have infinity distance at the beginning
        start.distance =0;

        // a comparator object to deal with Priority Queue
        Comparator<Node> adjacencyComparator = (left, right) -> {
            if (left.distance > (right.distance)) {
                return 1;
            }
            return -1;
        };

        // Queue to store visiting nodes
        Queue<Node> queueB = new PriorityQueue(size, adjacencyComparator);

        queueB.add(start);

        while (queueB.size() > 0) {
            Node current = queueB.remove();
            Node t;

            // Top
            if (current.x - 1 >= 0) {

                // Top Top
                t = gridArea[current.x - 1][current.y];
                if (!t.visited && !t.blocked && t.distance > current.distance + hVDistance) {
                    t.distance = current.distance + hVDistance;
                    t.parent = current;
                    queueB.add(t);
                }

                // Top Left
                if (current.y - 1 > 0) {
                    t = gridArea[current.x - 1][current.y - 1];
                    if (!t.visited && !t.blocked && t.distance > current.distance + dDistance) {
                        t.distance = current.distance + dDistance;
                        t.parent = current;
                        queueB.add(t);
                    }
                }

                // Top Right
                if (current.y + 1 < size) {
                    t = gridArea[current.x - 1][current.y + 1];
                    if (!t.visited && !t.blocked && t.distance > current.distance + dDistance) {
                        t.distance = current.distance + dDistance;
                        t.parent = current;
                        queueB.add(t);
                    }
                }
            }

            // Left
            if (current.y - 1 > 0) {
                t = gridArea[current.x][current.y - 1];
                if (!t.visited && !t.blocked && t.distance > current.distance + hVDistance) {
                    t.distance = current.distance + hVDistance;
                    t.parent = current;
                    queueB.add(t);
                }
            }

            // Right
            if (current.y + 1 < size) {
                t = gridArea[current.x][current.y + 1];
                if (!t.visited && !t.blocked && t.distance > current.distance + hVDistance) {
                    t.distance = current.distance + hVDistance;
                    t.parent = current;
                    queueB.add(t);
                }
            }
            // Down
            if (current.x + 1 < size) {

                // Down Down
                t = gridArea[current.x + 1][current.y];
                if (!t.visited && !t.blocked && t.distance > current.distance + hVDistance) {
                    t.distance = current.distance + hVDistance;
                    t.parent = current;
                    queueB.add(t);
                }

                // Down Left
                if (current.y - 1 >= 0) {
                    t = gridArea[current.x + 1][current.y - 1];
                    if (!t.visited && !t.blocked && t.distance > current.distance + dDistance) {
                        t.distance = current.distance + dDistance;
                        t.parent = current;
                        queueB.add(t);
                    }
                }

                // Down Right
                if (current.y + 1 < size) {
                    t = gridArea[current.x + 1][current.y + 1];
                    if (!t.visited && !t.blocked && t.distance > current.distance + dDistance) {
                        t.distance = current.distance + dDistance;
                        t.parent = current;
                        queueB.add(t);
                    }
                }
            }
            current.visited = true;
        }

        ArrayList<Node> path = new ArrayList<>();

        // Checking if a path exists
        if (!(gridArea[end.x][end.y].distance == Integer.MAX_VALUE)) {
            //Trace back the path
            Node current = gridArea[end.x][end.y];

            while (current.parent != null) {
                path.add(current.parent);
                current = current.parent;
            }
        } else System.out.println("No possible path");

        return path;
    }


    class Node {
        int x;
        int y;
        double distance = Integer.MAX_VALUE;
        Node parent = null;
        boolean visited;
        boolean blocked;

        public Node(int x, int y) {
            this.x = x;
            this.y = y;
        }
    }
}


Integrating with the StdDraw framework

The framework randomly generates a 2 dimensional boolean array to store the grid. We have to pass this array as the parameter to our algorithm.

 ArrayList<Dijkstra.Node> path = new Dijkstra().distance(randomlyGenMatrix, Ai, Aj, Bi, Bj);

This would return an Arraylist of Nodes of the minimum distance path.

All we have to do now is to draw the path in the grid given. Probably in a different color.

         StdDraw.setPenColor(Color.RED);

        for (Dijkstra.Node node : path) {
            StdDraw.circle(node.y, size - node.x - 1, .5);
        }

You have to repeat all these for three different distances. 

Notes

The framework given prints nodes in a weird manner. If you try to print a circle in first column second row (1,0), it actually prints at the bottom.


The three distances in question, Manhattan, Chebyshev and Euclidean  can easily be integrated in the algorithm. All you have to do, is to set
     horizontalVerticalDistance as 1
     diagonalDistance as 2
to get Manhattan Distance and
     horizontalVerticalDistance as 1
     diagonalDistance as 1
to get Chebyshev Distance.

These path finding problem can easily mapped to graph problems too. Consider the nodes as vertex and imaginary edges between them. The various distances will be the weight of the edges. This would help in finding the growth rate of the algorithm.

Comments

Post a Comment

Popular posts from this blog

Ace IIT Programming Principles Courseworks

Image
The blog is migrated to  https://thiloshon.wordpress.com   IIT is in my opinion a coursework-driven university where students believe they can learn more in the last two days before submission than in the entire lectures. At IIT programming is taught from the first day itself and I have seen students trying and failing to grasp the sense of programming and proper programming practices despite of lecturers trying all their best to provide students what they need. So this is from my experience of how to get good grades in 1st year CWs and to build on top of what you learned at IIT. Lecturers teach everything there is to get good grade and be a good programmer. If you listened to all the programming and design lectures and attended all the tutorials, then this blog is not probably for you. You know all this. For others, see if this makes sense. This is the first part of 2-part blog. 2nd part covers 2nd CW. Note: I’m using and recommending IntelliJ IDEA as the IDE and f
Read more

Web Service, Implementing a

Image
The blog is migrated to https://thiloshon.wordpress.com     Web Services are the most important elements of service oriented communication over the Internet. Knowing the underlying concepts of web services and how it has evolved over the time is very much expected from programmers. We might know pure Java or any other languages top to bottom but if we don’t know how its implemented in an industry or enterprise scenario there is not much use in what we learned. In the previous blog I covered many concepts and theories behind web services. In this blog let’s build a simple calculator web service in Java using GlassFish as application server and SOAP as the protocol. Let’s dive in. Building a web service I am using Netbeans in this blog since its very convenient to configure GlassFish server. IntelliJ IDEA can be used too but integrating server is a bit tedious. In the Netbeans create a new project. Select ‘Java Web’ as Category and ‘Web Application’ as Project. Click ‘Nex
Read more

Web Services, The Theories and Concepts of

The blog is migrated to  https://thiloshon.wordpress.com          Web Services are the most important elements of service oriented communication over the Internet.  Knowing the underlying concepts of web services and how it has evolved over the time is very much expected from programmers. We might know pure Java or any other languages top to bottom but if we don’t know how it's implemented in an industry or enterprise scenario there is not much use in what we learned. In this blog I cover many concepts and theories behind web services. In the subsequent blog  I'll cover how to build one in Java using GlassFish as application server and SOAP as the protocol. Let’s dive in. What is a web service? Let’s start with a simple scenario. You go to HSBC in Kollupitiya and deposit 50 000 to your account. And then you go to HSBC in Wellawatta and try to get that 50 000 back. Can you get your money back? Of course you can. But you deposited in a different branch right? H
Read more

A List of Royalists and Thomians in the Corporate World

A List of Royalists and Thomians in the corporate world. As of 2013 August Suren Amarasekera - CEO of Mobitel - Royalist Dr. Hans Wijayasuriya - CEO - Dialog Axiata - Thomian Mahendra Amarasuriya - Chairman Commercial Bank - Royalist Sir Ernest De Silva - founding Chairman of the Bank of Ceylon - Royalist Sir Cyril de Zoysa - Founder of the AMW group - Royalist Upali Wijewardene - Recorded Richest Sri Lankan to date - Royalist Janak Hidramani - Chairman of Hidramani Group - Thomian Sanjaya Padmaperuma - CEO - South Asian Technologies - Thomian Eraj Wijesinghe - Chairman Bartleet Group - Royalist Sunil C. Wijsinghe - Deputy Chairman Bartleet Group - Royalist Indrajith Fernando - CEO - Bartleet Group - Thomian Sunil C. Wijsinghe - Deputy Chairman Bartleet Group - Royalist Rajan Yatawara - Chairman(Former), Hayleys Group - Thomian D. S. Jayasundera - Chairman(Former),Hayleys Group - Royalist Sunil Mendis - former Chairman Hayleys - Royalist N G Wickremaratne- Chairman
Read more

GSoC 2017 : Integrating biodiversity data curation functionality

Image
Any data used in data science analyses, either it be simple statistical inference-making or high end machine learnings, needs to meet certain qualities. Any dataset has 'Signal' the answer we are trying to find and 'Noise' the disturbances and anomalies in the data. The important part of preparing data for analysis is to make it easier to distinguish signal from noise. In biodiversity researches, data can be very huge. Thus there is a high probability of having a lot of noise. Giving researchers control to reduce this noise will provide a clean and tidy data. Biodiversity research is a huge spectrum. It varies from analyzing simple heredity, climate and Eco-system impacts on species to complex Genome Sequencing researches. So the requirements of data in each of these fields vary with the type of researches. Taxonomic researchers will be interested in taxonomic fields and not so in spatial or temporal aspects of the data. They will be okay with loosing spatial data
Read more

How Dreams Work

   Did anyone see the movie Inception?  Well I did . And I got this awful feeling about dreams. Can I get robbed by dreams? And I couldn't just lay on the bed pondering to myself. So I just took the tab and googled. And I got this. I'm sharing it to you. See ya. How Dreams Work by Lee Ann Obringer        Our dreams combine verbal, visual and emotional stimuli into a sometimes broken, nonsensical but often entertaining story line. We can sometimes even solve problems in our sleep. Or can we? Many experts disagree on exactly what the purpose of our dreams might be. Are they strictly random brain impulses, or are our brains actually working through issues from our daily life while we sleep -- as a sort of coping mechanism? Should we even bother to interpret our dreams? Many say yes, that we have a great deal to learn from our dreams. In this article, we'll talk about the major dream theories, from Freud's view to the hypotheses that claim we can control our dr
Read more

A Kid with Leukemia.

Hello, Hi there. Its me once again. I got pretty interested in the decease Leukemia recently. This is a terrible stuff that kills children very silently. But we do have highly sophisticated treatment systems now. And I just thought of sharing this story of a leukemia kid who survived until now. Hope you like it too. 13 August 2013
Read more